
COLEGIO DE
BACHILLERES DEL ESTADO DE OAXACA
PLANTEL 04 “EL TULE”
“PROBABILIDAD Y ESTADISTICA”
ESTUDIANTE:
ALARCON REYES LUIS ANGEL
GRUPO: 633
ASESOR
ARQ. ALEJANDRO ENRIQUE VÁSQUEZ MARTÍNEZ
OAXACA DE JUAREZ OAX, ABRIL DEL 2013
ANALIZA Y RESUELVE SITUACIONES BASICAS DE PROBABILIDAD
Teoría
de conjuntos
La teoría de conjuntos es una rama de las
matemáticas
que estudia las propiedades
de los conjuntos:
colecciones abstractas de objetos, consideradas como objetos en sí mismas. Los
conjuntos y sus operaciones más elementales son una herramienta básica en la
formulación de cualquier teoría matemática.1
Sin embargo, la teoría de los
conjuntos es lo suficientemente rica como para construir el resto de objetos y
estructuras de interés en matemáticas: números,
funciones, figuras geométricas, ...; y junto con la lógica permite estudiar los fundamentos de
esta. En la actualidad se acepta que el conjunto de axiomas de la teoría de Zermelo-Fraenkel es suficiente
para desarrollar toda la matemática.
Álgebra de conjuntos
Existen
unas operaciones básicas que permiten manipular los
conjuntos y sus elementos, similares a las operaciones aritméticas, constituyendo el álgebra de conjuntos:
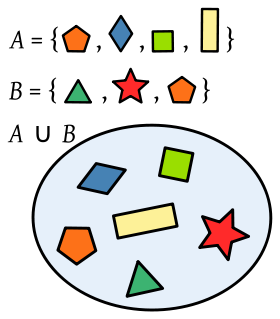 Unión. La unión de dos conjuntos A y B es el conjunto A
∪ B
que contiene cada elemento que está por lo menos en uno de ellos.
Unión. La unión de dos conjuntos A y B es el conjunto A
∪ B
que contiene cada elemento que está por lo menos en uno de ellos.
·
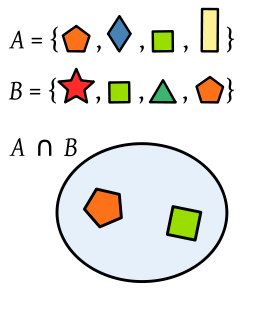
Intersección. La intersección de dos conjuntos A y B es el conjunto A
∩ B que contiene todos los
elementos comunes de A y B
- Diferencia. La diferencia entre dos conjuntos A y B es el conjunto A \ B que contiene todos los elementos de A que no pertenecen a B.
- Complemento. El complemento de un conjunto A es el conjunto A∁ que contiene todos los elementos (respecto de algún conjunto referencial) que no pertenecen a A.

- Diferencia simétrica La diferencia simétrica de dos conjuntos A y B es el conjunto A Δ B con todos los elementos que pertenecen, o bien a A, o bien a B, pero no a ambos a la vez.

- Producto cartesiano. El producto cartesiano de dos conjuntos A y B es el conjunto A × B que contiene todos los pares ordenados (a, b) cuyo primer elemento a pertenece a A y su segundo elemento b pertenece a B.
CONCEPTOS BÁSICOS DE
PROBABILIDAD
Experimento. Cualquier acción cuyo resultado se
registra como un dato.
Espacio Muestral (S). El conjunto de todos los posibles resultados de un experimento.
Ejemplo.
Al lanzar un dado equilibrado se pueden observar los resultados
siguientes:
E = {1, 2, 3, 4, 5, 6} E = {6}
E = {1, 2, 3, 4, 5, 6} E = {6}
Ejemplo.
En el lanzamiento de dos monedas tenemos;
E = {SS, SA, AS, AA} E = {4}
E = {SS, SA, AS, AA} E = {4}
Evento. Son los resultados obtenidos de
realizar un experimento. Cuándo cada evento es seleccionado al azar, el
experimento se denomina aleatorio o al azar.
experimento se denomina aleatorio o al azar.
Evento Simple (E). Cada uno de los posibles resultados
de un experimento y que no se puede descomponer.
Ejemplo:
En el caso del lanzamiento del dado, cada uno de los posibles números en la
cara del dado es un evento simple.
Experimento aleatorio: conjunto de pruebas cuyos
resultados están determinados únicamente por el azar.
Punto muestral o suceso elemental: el resultado de una sola prueba
de un experimento muestral
Sucesos mutuamente excluyentes: sucesos o eventos que no pueden
ocurrir simultáneamente.
Sucesos complementarios: dos sucesos o eventos mutuamente
excluyentes cuya unión es el espacio muestral
Sucesos independientes: sucesos o eventos que no tienen
relación entre sí; la ocurrencia de uno no afecta la ocurrencia del otro
Sucesos dependientes: sucesos o eventos que sí tienen
relación entre sí; la ocurrencia de uno sí afecta la ocurrencia del otro.
TECNICAS DE CONTEO
El
principio fundamental en el proceso de contar ofrece un método general para
contar el número de posibles arreglos de objetos dentro de un solo conjunto o
entre carios conjuntos. Las técnicas de conteo son aquellas que son usadas para
enumerar eventos difíciles de cuantificar.
Si un evento A puede ocurrir de n1 maneras y una vez que este ha
ocurrido, otro evento B puede n2 maneras
diferentes entonces, el número total de formas diferentes en que ambos eventos
pueden ocurrir en el orden indicado, es igual a n1 x n2.
¿De cuántas maneras pueden repartirse
3 premios a un conjunto de 10 personas, suponiendo que cada persona no puede
obtener más de un premio?
Aplicando el principio
fundamental del conteo, tenemos 10 personas que pueden recibir el primer premio.
Una vez que éste ha sido entregado, restan 9 personas para recibir el segundo,
y posteriormente quedarán 8 personas para el tercer premio. De ahí que el
número de maneras distintas de repartir los tres premios.
n10
x 9 x 8 = 720
¿Cuántas
placas de automóvil se pueden hacer utilizando dos letras seguidas de tres
cifras? No se admiten repeticiones.
26
x 25 x 10 x 9 x 8 = 468000 n un número entero positivo, el producto n (n-1) (n-2)...3
x 2 x 1 se llama factorial de n.
El
símbolo ! se lee factorial
y es el producto resultante de todos los enteros positivos de 1 a n; es decir,
sea
n5!
= 5 x 4 x 3 x 2 x 1 = 120
Por
definición 0! = 1
Si
el número de posibles resultados de un experimento es pequeño, es relativamente
fácil listar y contar todos los posibles resultados. Al tirar un dado, por
ejemplo, hay seis posibles resultados.
Si, sin embargo, hay un gran número de posibles resultados tales como el número de niños y niñas por familias con cinco hijos, sería tedioso listar y contar todas las posibilidades. Las posibilidades serían, 5 niños, 4 niños y 1 niña, 3 niños y 2 niñas, 2 niños y 3 niñas, etc.
Para
facilitar el conteo examinaremos las siguientes técnicas:
PRINCIPIO DE LA MULTIPLICACION
Si se desea realizar una actividad que consta de r pasos, en donde el primer paso de la actividad a realizar puede ser llevado a cabo de N1 maneras o formas, el segundo paso de N2 maneras o formas y el r-ésimo paso de Nr maneras o formas, entonces esta actividad puede ser llevada a efecto de. El principio multiplicativo implica que cada uno de los pasos de la actividad deben ser llevados a efecto, uno tras otro. Si un evento E1 puede suceder de n1 maneras diferentes, el evento E2 puede ocurrir de n2 maneras diferentes, y así sucesivamente hasta el evento Ep el cual puede ocurrir de np maneras diferentes, entonces el total de maneras distintas en que puede suceder el evento “ocurren E1 y E2…..y Ep” es igual a producto.
N1 x N2 x ..........x Nr maneras o formas
Ejemplo:
Se dispone de 3 vías para viajar de C1 a C2 y de 4 vías para viajar de C2 a C1. ¿De cuántas formas se puede organizar el viaje de ida y vuelta de C1 a C2.Respuesta: (3)(4)=12
Se dispone de 3 vías para viajar de C1 a C2 y de 4 vías para viajar de C2 a C1. ¿De cuántas formas se puede organizar el viaje de ida y vuelta de C1 a C2.Respuesta: (3)(4)=12
PRINCIPIO ADITIVO.
Si
se desea llevar a efecto una actividad, la cuál tiene formas alternativas para
ser realizada, donde la primera de esas alternativas puede ser realizada de M
maneras o formas, la segunda alternativa puede realizarse de N maneras o formas
..... y la última de las alternativas puede ser realizada de W maneras o
formas, entonces esa actividad puede ser llevada a cabo de,
M + N + .........+ W maneras o formas
Ejemplos:
1)
Una persona desea comprar una lavadora de ropa, para lo cuál ha pensado que
puede seleccionar de entre las marcas Whirpool, Easy y General Electric, cuando
acude a hacer la compra se encuentra que la lavadora de la marca W se presenta
en dos tipos de carga ( 8 u 11 kilogramos), en cuatro colores diferentes y
puede ser automática o semiautomática, mientras que la lavadora de la marca E,
se presenta en tres tipos de carga (8, 11 o 15 kilogramos), en dos colores
diferentes y puede ser automática o semiautomática y la lavadora de la marca
GE, se presenta en solo un tipo de carga, que es de 11 kilogramos, dos colores
diferentes y solo hay semiautomática. ¿Cuántas maneras tiene esta persona de
comprar una lavadora?
Solución:
M
= Número de maneras de seleccionar una lavadora Whirpool
N
= Número de maneras de seleccionar una lavadora de la marca Easy
W
= Número de maneras de seleccionar una lavadora de la marca General Electric
M = 2 x 4 x 2 = 16 maneras
N
= 3 x 2 x 2 = 12 maneras
W
= 1 x 2 x 1 = 2 maneras
M
+ N + W = 16 + 12 + 2 = 30 maneras de seleccionar una lavadora
PRINCIPIO DE LA SUMA O ADICCION
Si
una primera operación puede realizarse de m maneras y una segunda operación de
n maneras, entonces una operación o la otra pueden efectuarse de:
m+n maneras.
Ejemplo:
Una
pareja que se tiene que casar, junta dinero para el enganche de su casa, en el
fraccionamiento lomas de la presa le ofrecen un modelo económico ó un
condominio, en el fraccionamiento Playas le ofrecen un modelo económico como
modelos un residencial, un californiano y un provenzal. ¿Cuántas alternativas
diferentes de vivienda le ofrecen a la pareja?
PRESA
PLAYAS
Económico
Residencial
Condominio
Californiano
Provenzal
m=2
n=3
2+3= 5 maneras
PRINCIPIO DE
PERMUTACION:
A diferencia de la formula de la multiplicación, se la utiliza para determinar el número de posibles arreglos cuando solo hay un solo grupo de objetos. Permutación: un arreglos o posición de r objetos seleccionados de un solo grupo de n objetos posibles. Si nos damos cuenta los arreglos a, b, c y b, a, c son permutaciones diferentes, la formula que se utiliza para contar el número total de permutaciones distintas es:
A diferencia de la formula de la multiplicación, se la utiliza para determinar el número de posibles arreglos cuando solo hay un solo grupo de objetos. Permutación: un arreglos o posición de r objetos seleccionados de un solo grupo de n objetos posibles. Si nos damos cuenta los arreglos a, b, c y b, a, c son permutaciones diferentes, la formula que se utiliza para contar el número total de permutaciones distintas es:
FÓRMULA: n P r = n! (n - r)
Ejemplo: ¿Cómo se puede designar los cuatro primeros lugares de un concurso, donde existen 15 participantes?
Aplicando la formula de la permutación tenemos:
Ejemplo: ¿Cómo se puede designar los cuatro primeros lugares de un concurso, donde existen 15 participantes?
Aplicando la formula de la permutación tenemos:
n P r = n! (n - r)! = 15! = 15*14*13*12 *11*10*9*8*7*6*5*4*3*2*1 (15-4)! 11*10*9*8*7*6*5*4*3*2*1 = 32760
Donde:
n= número total de objetos r= número de objetos seleccionados!= factorial,
producto de los números naturales entre 1 y n.
NOTA: se puede cancelar números cuando se tiene las mismas cifras en numerador y denominador. !
PRINCIPIO DE COMBINACION:
En una permutación, el orden de los objetos de cada posible resultado es diferente. Si el orden de los objetos no es importante, cada uno de estos resultados se denomina combinación. Por ejemplo, si se quiere formar un equipo de trabajo formado por 2 personas seleccionadas de un grupo de tres (A, B y C). Si en el equipo hay dos funciones diferentes, entonces si importa el orden, los resultados serán permutaciones. Por el contrario si en el equipo no hay funciones definidas, entonces no importa el orden y los resultados serán combinaciones. Los resultados en ambos casos son los siguientes:
NOTA: se puede cancelar números cuando se tiene las mismas cifras en numerador y denominador. !
PRINCIPIO DE COMBINACION:
En una permutación, el orden de los objetos de cada posible resultado es diferente. Si el orden de los objetos no es importante, cada uno de estos resultados se denomina combinación. Por ejemplo, si se quiere formar un equipo de trabajo formado por 2 personas seleccionadas de un grupo de tres (A, B y C). Si en el equipo hay dos funciones diferentes, entonces si importa el orden, los resultados serán permutaciones. Por el contrario si en el equipo no hay funciones definidas, entonces no importa el orden y los resultados serán combinaciones. Los resultados en ambos casos son los siguientes:
Permutaciones:
AB, AC, BA, CA, BC, CB
Combinaciones:
AB, AC, BC
Combinaciones: Es el número de formas de seleccionar r objetos de un grupo de n objetos sin importar el orden.
La fórmula de combinaciones es:
n C r = n! r! (n – r)!
Ejemplo: En una compañía se quiere establecer un código de colores para identificar cada una de las 42 partes de un producto. Se quiere marcar con 3 colores de un total de 7 cada una de las partes, de tal suerte que cada una tenga una combinación de 3 colores diferentes. ¿Será adecuado este código de colores para identificar las 42 partes del producto?
Usando la fórmula de combinaciones:
n C r = n! = 7! = 7! = 35
r! (n – r )! 3! (7 – 3)! 3! 4!
El tomar tres colores de 7 posibles no es suficiente para identificar las 42 partes del producto.
APLICA LA PROBABILIDAD SIMPLE Y CONJUNTA
EVENTOS
INDEPENDIENTES
Cuando se lanza una moneda repetidamente y se obtiene 5 veces corridas cara , podría decirse que la posibilidad, o probabilidad, de obtener cara en el próximo lanzamiento es muy pequeña. Después de todo, la posibilidad de obtener 6 caras corridas es muy pequeña. O, se puede pensar que la posibilidad de obtener cara en el próximo lanzamiento es grande; hay una “corrida” de caras. De hecho, sin embargo, la moneda no tiene memoria; la posibilidad de obtener cara en el próximo lanzamiento es 0.5, al igual que lo ha sido todo el tiempo. Se podría decir que los eventos son independientes; el resultado del sexto lanzamiento no depende del resultado del quinto lanzamiento.
Cuando se lanza una moneda repetidamente y se obtiene 5 veces corridas cara , podría decirse que la posibilidad, o probabilidad, de obtener cara en el próximo lanzamiento es muy pequeña. Después de todo, la posibilidad de obtener 6 caras corridas es muy pequeña. O, se puede pensar que la posibilidad de obtener cara en el próximo lanzamiento es grande; hay una “corrida” de caras. De hecho, sin embargo, la moneda no tiene memoria; la posibilidad de obtener cara en el próximo lanzamiento es 0.5, al igual que lo ha sido todo el tiempo. Se podría decir que los eventos son independientes; el resultado del sexto lanzamiento no depende del resultado del quinto lanzamiento.
EVENTOS DEPENDIENTES
Eventos
dependientes
Dos o más eventos serán dependientes cuando la ocurrencia o no-ocurrencia de uno de ellos afecta la probabilidad de ocurrencia del otro (o otros). Cuando tenemos este caso, empleamos entonces, el concepto de probabilidad condicional para denominar la probabilidad del evento relacionado. La expresión P(AB) indica la probabilidad de ocurrencia del evento A sí el evento B ya ocurrió.
Se debe tener claro que AB no es una fracción.
P(AB) = P(A y B)/P(B) o P(BA) = P(A y B)/P(A)
Dos o más eventos serán dependientes cuando la ocurrencia o no-ocurrencia de uno de ellos afecta la probabilidad de ocurrencia del otro (o otros). Cuando tenemos este caso, empleamos entonces, el concepto de probabilidad condicional para denominar la probabilidad del evento relacionado. La expresión P(AB) indica la probabilidad de ocurrencia del evento A sí el evento B ya ocurrió.
Se debe tener claro que AB no es una fracción.
P(AB) = P(A y B)/P(B) o P(BA) = P(A y B)/P(A)
EVENTOS
MUTUAMENTE EXCLUYENTES Y NO EXCLUYENTES
Dos o más eventos son mutuamente excluyentes o disjuntos, si no pueden ocurrir simultáneamente. Es decir, la ocurrencia de un evento impide automáticamente la ocurrencia del otro evento (o eventos).
Ejemplo:
Al lanzar una moneda solo puede ocurrir que salga cara o cruz pero no los dos a la vez, esto quiere decir que estos eventos son excluyentes.
Dos o más eventos son no excluyentes, o conjuntos, cuando es posible que ocurran ambos. Esto no indica que necesariamente deban ocurrir estos eventos en forma simultánea
Dos o más eventos son mutuamente excluyentes o disjuntos, si no pueden ocurrir simultáneamente. Es decir, la ocurrencia de un evento impide automáticamente la ocurrencia del otro evento (o eventos).
Ejemplo:
Al lanzar una moneda solo puede ocurrir que salga cara o cruz pero no los dos a la vez, esto quiere decir que estos eventos son excluyentes.
Dos o más eventos son no excluyentes, o conjuntos, cuando es posible que ocurran ambos. Esto no indica que necesariamente deban ocurrir estos eventos en forma simultánea
Ejemplo:
Si consideramos en un juego de domino sacar al menos un blanco y un seis, estos eventos son no excluyentes porque puede ocurrir que salga el seis blanco.
Si consideramos en un juego de domino sacar al menos un blanco y un seis, estos eventos son no excluyentes porque puede ocurrir que salga el seis blanco.
PROBABILIDAD
SIMPLE, CONJUNTA Y CONDICIONAL
La probabilidad simple, determina la probilidad de
ocurra un evento especifico durante un experimento o de un conjunto de
información proporcionada.
Ejemplo:
Ejemplo:
Hay 87 canicas en una bolsa y 68 son verdes. Si se escoge una, ¿cuál es la
probabilidad de que esta sea verde?
Solución:
- Divide la cantidad de formas de elegir una canica verde (68) por la cantidad total de canicas (87)
- 68 ÷ 87 = 0.781609
- Redondea a la precisión deseada (es decir 0.781609 redondeado a centésimos es 0.78
La probabilidad conjunta se da cuanto se requiere que dos
eventos ocurran de manera simultánea y existen dos casos:
- En el caso que los eventos sean mutuamente excluyentes es decir que uno impida la ocurrencia del otro, en este caso la probabilidad se determina de la siguiente manera:
P(A o B)
= P(A) + P (B)
- En el caso que los eventos sean no excluyentes, es decir que uno no interfiera con la ocurrencia del otros se determina
P(A o B)=
P(A) + P(B) – P(A y B)
La probabilidad condicional, calcula la probabilidad de que
ocurra un evento (A), dado que ya ocurrió un evento (B) y se determina
mediante:
P(A/B) =
P(A y B) / P (B)
COMPRENDE, REPRESENTA Y APLICA LA PROBABILIDAD CONDICIONAL Y DISTRIBUCION DE VARIABLES ALEATORIAS DISCRETAS
FUNCIONES
DE PROBABILIDAD DISCRETAS
La
distribución de probabilidad para una variable aleatoria discreta puede ser:
1.- Una
relación teórica de resultados y probabilidades que se puede obtener de un
modelo matemático y que representa algún fenómeno de interés.
2.- Una
relación empírica de resultados y sus frecuencias relativas observadas.
3.- Una
relación subjetiva de resultados relacionados con sus probabilidades subjetivas
o artificiales que representan el grado de convicción del encargado en tomar
decisiones sobre la probabilidad de posibles resultados.
Sabemos
que una variable aleatoria discreta o discontinua es aquella en la que existe
una distancia bien definida entre dos de los valores consecutivos que asume; y
dichos valores son numerables.
Existen
varios modelos matemáticos que representan diversos fenómenos discretos de la
vida real.
Las más
útiles son:
1.- La
distribución uniforme discreta.
1.- La
distribución de probabilidad Binomial o de Bernoulli.
2.- La
distribución de probabilidad Hipergeométrica.
3.- La
distribución de probabilidad de Poisson.
UNIFORME DISCRETA
Si la
variable aleatoria X Asume valores de X1, X2, ..., Xk con iguales probabilidades,
entonces la distribución uniforme es:
f (x, k) = 1/K
LA DISTRIBUCION BINOMIAL
Esta
distribución fue elaborada por Jacobo Bernoulli y es aplicable a un gran número
de problemas de carácter económico y en numerosas aplicaciones como:
- Juegos
de azar.
- Control
de calidad de un producto.
- En
educación.
- En las
finanzas.
La distribución
Binomial posee las siguientes propiedades esenciales:
1.- El
espacio muestral contiene n ensayos idénticos.
2.- Las
observaciones posibles se pueden obtener mediante dos diferentes métodos de
muestreo. Se puede considerar que cada observación se ha seleccionado de una
población infinita sin reposición o de una población finita con reposición.
3.- Cada
observación se puede clasificar en una de dos categorías conocidas como éxito E
o fracaso E', las cuales son mutuamente excluyentes es decir E ∩ E' = 0.
4.- Las
probabilidades de éxito p y de fracaso q = 1 - p en un ensayo se mantienen
constantes, durante los n ensayos.
5.- El
resultado de cualquier observación es independiente del resultado de cualquier
otra observación.
La
probabilidad de que el evento E ocurra x veces y el evento E' ocurra (n x) veces
en n ensayos independientes está dado por la fórmula Binomial:

n es el número de pruebas.
k es el número de éxitos.
p es la probabilidad de éxito.
q es la probabilidad de fracaso.
Media
Varianza
Desviación típica
LA DISTRIBUCION
Características:
a)
Al
realizar un experimento con este tipo de distribución, se esperan más de dos
tipos de resultados.
b)
Las
probabilidades asociadas a cada uno de estos resultados no son constantes.
c)
Los
ensayos o repeticiones del experimento no son independientes entre sí.
d)
El
número de repeticiones del experimento n, es constante.
Entonces en este caso se
tienen más de dos tipos de objetos, por lo que la fórmula a utilizar sería:
donde:
N = x + y + z = total de
objetos
a = total de objetos del
primer tipo
b = total de objetos del
segundo tipo
c = N-a-b = total de objetos
del tercer tipo
n = objetos seleccionados en
la muestra
x = objetos del primer tipo
en la muestra
y = objetos del segundo tipo
en la muestra
z = n-x-y = objetos del
tercer tipo en la muestra
Ejemplos:
1.En un lote de productos se
tienen 20 productos sin defectos, 3 con defectos menores y 2 con defectos
mayores, se seleccionan al azar 5 productos de este lote, determine la
probabilidad de que a) 3 de los productos seleccionados no tengan defectos y 1
tenga defectos menores, b) 4 de los productos seleccionados no tengan defectos
y 1 tenga defectos menores.
Solución:
a)N= 20+3+2 =25 total de artículos
a=20 productos sin defectos
b= 3 productos con defectos
menores
N-a-b= 2 productos con
defectos mayores
n= 5 productos seleccionados
en la muestra
x = 3 productos sin defectos
en la muestra = variable que nos define el # de productos sin defectos en la
muestra
y = 1 producto con defectos
menores en la muestra = variable que nos define el # de productos con defectos menores en la muestra
z = n-x-y = 5-3-1 = 1
producto con defectos mayores en la muestra = variable que nos define el # de
productos con defectos mayores en la muestra
b)N= 25
a=20 productos sin defectos
b= 3 productos con defectos
menores
N-a-b= 2 productos con
defectos mayores
n= 5 productos seleccionados
en la muestra
x = 4 productos sin defectos
en la muestra = variable que nos define el # de productos sin defectos en la
muestra
y = 1 producto con defectos
menores en la muestra = variable que nos define el # de productos con defectos menores en la muestra
z = n-x-y = 5-4-1 = 0
productos con defectos mayores en la muestra = variable que nos define el # de
productos con defectos mayores en la muestra

3.Un club de estudiantes
extranjeros tiene en sus listas a 2 canadienses, 3 japoneses, 5 italianos y 2
alemanes. Si se selecciona aleatoriamente un comité de 4 estudiantes, encuentre
la probabilidad de que: a)estén representadas todas las nacionalidades, b)estén
representadas todas las nacionalidades, excepto la italiana.
Solución:
a) N = 12 estudiantes
a = 2 Canadienses
b = 3 Japoneses
c = 5 Italianos
N-a-b-c = 2 Alemanes
n = 4 estudiantes
seleccionados para formar comité
x = 1 estudiante Canadiense
en el comité seleccionado
y = 1 estudiante Japonés en
el comité seleccionado
z = 1 estudiante Italiano en
el comité seleccionado
n-x-y-z = 1 estudiante
Alemán en el comité seleccionado

b) N = 7 estudiantes
quitando a los Italianos
a = 2 Canadienses
b = 3 Japoneses
N-a-b = 2 Alemanes
n = 4 estudiantes
seleccionados para formar comité
x = 1 o 2 estudiantes
Canadienses en el comité seleccionado
y = 1 o 2 estudiantes
Japoneses en el comité seleccionado
n-x-y= 1 o 2 estudiantes
Alemanes en el comité seleccionado
p(estén representadas todas
las nacionalidades, excepto la italiana)

La distribución de Poisson
Se trata de un modelo discreto, pero en el que
el conjunto de valores con probabilidad no nula no es finito, sino numerable. Se
dice que una variable aleatoria X sigue la distribución de Poisson si su
función de densidad viene dada por:

Propiedades del modelo de Poisson
1) Esperanza: E(X) = λ.
2) Varianza: V(X) = λ.
En esta distribución la esperanza y la varianza coinciden.
3) La suma de dos variables aleatorias
independientes con distribución de Poisson resulta en una nueva variable
aleatoria, también con distribución de Poisson, de parámetro igual a la suma de
parámetros:
X1 ~
P(λ = λ1) y X2 ~ P(λ =
λ2)
y definimos Z = X1 + X2,
entonces,
Z ~ P(λ = λ1
+ λ2)
Este resultado se extiende inmediatamente al caso
de n variables aleatorias independientes con distribución de Poisson. En este
caso, la variable suma de todas ellas sigue una distribución de Poisson de
parámetro igual a la suma de los parámetros.
Media aritmética
Construcción geométrica para hallar las medias aritmética, geométrica y armónica de dos números a y b.
Expresada de forma más intuitiva, podemos decir que la media (aritmética) es la cantidad total de la variable distribuida a partes iguales entre cada observación.
Por ejemplo, si en una habitación hay tres personas, la media de dinero que tienen en sus bolsillos sería el resultado de tomar todo el dinero de los tres y dividirlo a partes iguales entre cada uno de ellos. Es decir, la media es una forma de resumir la información de una distribución (dinero en el bolsillo) suponiendo que cada observación (persona) tuviera la misma cantidad de la variable.
También la media aritmética puede ser denominada como centro de gravedad de una distribución, el cual no está necesariamente en la mitad.
Una de las limitaciones de la media aritmética es que se trata de una medida muy sensible a los valores extremos; valores muy grandes tienden a aumentarla mientras que valores muy pequeños tienden a reducirla, lo que implica que puede dejar de ser representativa de la población.
Definición
Dados los n números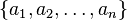 , la media aritmética se define como:
, la media aritmética se define como:Por ejemplo, la media aritmética de 8, 5 y -1 es igual a:
Se utiliza la letra X con una barra horizontal sobre el símbolo para representar la media de una muestra (
 ), mientras que la letra µ (mu) se usa para la media aritmética de una población, es decir, el valor esperado de una variable.
), mientras que la letra µ (mu) se usa para la media aritmética de una población, es decir, el valor esperado de una variable.En otras palabras, es la suma de n valores de la variable y luego dividido por n : donde n es el número de sumandos, o en el caso de estadística el número de datos.
Propiedades
- La suma de las desviaciones con respecto a la media aritmética es cero (0).
- La media aritmética de los cuadrados de las desviaciones de los valores de la variable con respecto a una constante cualquiera se hace mínima cuando dicha constante coincide con la media aritmética.
- Si a todos los valores de la variable se le suma una misma cantidad, la media aritmética queda aumentada en dicha cantidad.
- Si todos los valores de la variable se multiplican por una misma constante la media aritmética queda multiplicada por dicha constante.
- La media aritmética de un conjunto de números positivos siempre es igual o superior a la media geométrica:
- La media aritmética está comprendida entre el valor máximo y el valor mínimo del conjunto de datos:
LA DESVIACION ESTANDAR
La desviación estándar (DS/DE), también llamada desviación típica, es una medida de dispersión usada en estadística que nos dice cuánto tienden a alejarse los valores concretos del promedio en una distribución. De hecho, específicamente, la desviación estándar es "el promedio del cuadrado de la distancia de cada punto respecto del promedio". Se suele representar por una S o con la letra sigma, .
.La desviación estándar de un conjunto de datos es una medida de cuánto se desvían los datos de su media. Esta medida es más estable que el recorrido y toma en consideración el valor de cada dato.
Distribución de probabilidad continua
Es posible calcular la desviación estándar de una variable aleatoria continua como la raíz cuadrada de la integralDistribución de probabilidad discreta
La DS es la raíz cuadrada de la varianza de la distribución de probabilidad discretaAunque esta fórmula es correcta, en la práctica interesa realizar inferencias poblacionales, por lo que en el denominador en vez de n, se usa n-1 (Corrección de Bessel) Esta ocurre cuando la media de muestra se utiliza para centrar los datos, en lugar de la media de la población. Puesto que la media de la muestra es una combinación lineal de los datos, el residual a la muestra media se extiende más allá del número de grados de libertad por el número de ecuaciones de restricción - en este caso una. Dado esto a la muestra así obtenida de una muestra sin el total de la población se le aplica esta corrección con la fórmula desviación estándar muestral. Cuando los casos tomados son iguales al total de la población se aplica la fórmula de desviación estándar poblacional.
Ejemplo
Aquí se muestra cómo calcular la desviación estándar de un conjunto de datos. Los datos representan la edad de los miembros de un grupo de niños: { 4, 1, 11, 13, 2, 7 }1. Calcular el promedio o media aritmética
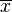 .
. .
.
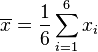 Sustituyendo N por 6
Sustituyendo N por 6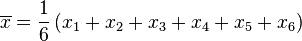
 Este es el promedio.
Este es el promedio.
2. Calcular la desviación estándar
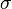
 Sustituyendo N - 1 por 5; ( 6 - 1 )
Sustituyendo N - 1 por 5; ( 6 - 1 )
 Sustituyendo
Sustituyendo 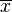 por 6,33
por 6,33
 Éste es el valor de la desviación estándar.
Éste es el valor de la desviación estándar.
EJERCICIOS
- Hay 87 canicas en una bolsa y 68 son verdes. Si se escoge una, ¿cuál es la probabilidad de que esta sea verde?
Solución:
Divide la cantidad de formas de elegir una canica verde (68) por la cantidad total de canicas (87)
68 ÷ 87 = 0.781609
Redondea a la precisión deseada (es decir 0.781609 redondeado a centésimos es 0.78
- Si yo tengo una canasta llena de peras y manzanas, de las cuales hay 20 peras y 10 manzanas. ¿Qué fruta es más probable que saque al azar de la canasta?
Para este ejemplo tenemos que 30 es el total de frutas en la canasta; es decir los casos posibles. Para calcular la probabilidad de sacar una manzana mis casos favorables son 10 puesto que existen sólo 10 manzanas. Así, aplicando la fórmula obtenemos que:
P(Manzana)=10/30=1/3= 33.3% probable
Calculando igual, la probabilidad de sacar pera es:
P(Pera)=20/30=2/3= 66.7% probable
Como 66.7 es mayor que 33.3 es más probable que saque una pera, pues hay más peras que manzanas en la canasta.
- El 70% de empresas tiene errores en sus activos financieros, el 60% tiene errores en
sus pasivos financieros y el 40% tiene errores en sus activos y en sus pasivos
financieros. Obtén razonadamente el porcentaje de empresas sin errores en sus
activos, en sus pasivos o en ambos. De una muestra de 500 empresas, ¿cuántas se
espera que no tengan errores ni en sus activos ni en sus pasivos financieros?
Solución:
Llamemos A = {tener errores en los activos financieros} y B = {tener errores en los
pasivos financieros}. Entonces P(A) = 0’7, P(B) = 0’6 y P(A∩B) = 0’4.
El suceso “no tener errores en los activos financieros” es
A y por tanto P(A) = 1−P(A) = 1−0’7 = 0’3 lo que significa el 30%.
El suceso “no tener errores en los pasivos financieros” es By por tanto P(B) = 1−P(B) = 1−0’6 = 0’4 lo que significa el 40%. El suceso “no tener errores en ambos” equivale a “no tener errores en los activos
financieros y no tener errores en los pasivos financieros”, es decir,
A∩B. Pero, porlas leyes de Morgan,A∩B=BA∪. Entonces P(A∩B) = P(BA∪) = 1−P(AB) = 1−[P(A) + P(B)−P(A∩B)] = 1−(0’7 + 0’6−0’4) = 1−0’9 = 0’1 lo que significa un 10%.
Según lo anterior se espera que un 10% de las empresas no tengan errores ni en sus
activos ni en sus pasivos financieros. Si tenemos una muestra de 500 empresas
podemos esperar que 500 10/100= 50 empresas no tengan errores ni en sus activos ni
en sus pasivos financieros.
1. Sean A y B dos sucesos aleatorios con p(A) = 1/2, p(B) =
1/3, p(A  B)= 1/4. Determinar:
B)= 1/4. Determinar:
a. 

b.

c. )

2. En un centro escolar los alumnos pueden optar por cursar como lengua extranjera inglés o francés. En un determinado curso, el 90% de los alumnos estudia inglés y el resto francés. El 30% de los que estudian inglés son chicos y de los que estudian francés son chicos el 40%. El elegido un alumno al azar, ¿cuál es la probabilidad de que sea chica?
Sol.
Dibujando un
diagrama de árbol y Aplicando la regla de la multiplicación, tenemos:

La probabilidad de que sea una chicas es:
p(chica) = 0.9 · 0.7 + 0.1 · 0.6 = 0.69
3.
De una
baraja de 48 cartas se extrae simultáneamente dos de ellas. Calcular la
probabilidad de que:
a. Las dos sean copas.
Se
sabe que si el paquete es de 48 cartas, y tienes 4 pintas, entonces existen 12
barajas de cada pinta. Si el experimento se realiza sin reemplazo.
b. Al menos una sea copas.
Para garantizar que al escoger una baraja
al menos una sea copa se debe encontrar la probabilidad complemento, que es que no se escoja ninguna copa, así:
C. Una sea copa y la otra espada.
P(1c
∩1e)=P(1^a c ∩ 2^a e)+ P(1^a e ∩ 2^a c)=12/48*12/48+12/48*12/48=0.125
4.
Una clase
está formada por 10 chicos y 10 chicas; la mitad de las chicas y la mitad de
los chicos han elegido francés como asignatura optativa.
a.
¿Cuál es la
probabilidad de que una persona elegida al azar sea chico o estudio francés?
Utilicemos un diagrama de Venn para visualizar el
problema.
B: el evento
de que la persona elegida estudie francés
P(A U B)=P(A)+P(B)- P(A ∩
B)=10/20+10/20-(10/20*10/20)=15/20=0.75
También se puede escribir de la siguiente manera
directamente del diagrama de venn
b.
¿Y la
probabilidad de que sea chica y no estudie francés?
Sea C: el evento de que la persona elegida sea chica
D: el evento de que la
persona elegida NO estudie
francés.
Como son eventos dependientes:
P(C
∩ D)=P(C)*P(D/C)=10/20*10/20=5/20=0.25
También se pude haber escrito de la siguiente manera
directamente del diagrama de venn:
5.
Una urna
contiene 5 bolas rojas y 8 verdes. Se extrae una bola y se reemplaza por dos
del otro color. A continuación, se extrae una segunda bola. Se pide:
1. Probabilidad de que la segunda bola sea verde.
2. Probabilidad de que las dos bolas extraídas sean del mismo color.
6.
En una
estantería hay 60 novelas y 20 libros de poesía. Una persona A elige un libro
al azar de la estantería y se lo lleva. A continuación otra persona B elige
otro libro al azar.
1.
¿Cuál es la probabilidad de que el libro seleccionado por B sea una
novela?
Aplicando la regla de la multiplicación,
tenemos:
2.
Si se sabe
que B eligió una novela, ¿cuál es la probabilidad de que el libro seleccionado
por A sea de poesía?
Aplicando la formula el teorema de Bayes, tenemos:
7.
Una clase
consta de seis niñas y 10 niños. Si se escoge un comité de tres al azar, hallar
la probabilidad de:
a. Seleccionar tres niños.
b.
Seleccionar
exactamente dos niños y una niña.
c.
Seleccionar
por lo menos un niño.
d.
Seleccionar
exactamente dos niñas y un niño.
8.
El 20% de
los empleados de una empresa son ingenieros y otro 20% son economistas. El 75%
de los ingenieros ocupan un puesto directivo y el 50% de los economistas
también, mientras que los no ingenieros y los no economistas solamente el 20%
ocupa un puesto directivo. ¿Cuál es la probabilidad de que un empleado
directivo elegido al azar sea ingeniero?
Aplicando
el teorema de bayes:
9.
La
probabilidad de que haya un accidente en una fábrica que dispone de alarma es
0.1. La probabilidad de que suene esta sí se ha producido algún incidente es de
0.97 y la probabilidad de que suene si no ha sucedido ningún incidente es 0.02.
En el supuesto de que haya funcionado la
alarma, ¿cuál es la probabilidad de que no haya habido ningún incidente?
Sean los sucesos:
I = Producirse incidente.
A = Sonar la alarma.
Aplicando
el teorema de bayes:
e) La colección formada por el suceso A, el B, la unión de ambos, su intersección, y su
diferencia, más el suceso seguro y el suceso imposible, no constituye un
sigma-álgebra.
Para demostrarlo basta comprobar que se incumple una de las dos condiciones. Por
ejemplo, el suceso A incumple la segunda porque su contrario no pertenece a la
colección.
3- Una rata es colocada en una caja con tres pulsadores de colores rojo, azul y blanco. Si
pulsa dos veces las palancas al azar:
a)¿Cuál es la probabilidad de que las dos veces pulse la roja?
b)¿Cuál es la probabilidad de que pulse la primera vez o la segunda o ambas la tecla
azul?
Solución
a)Para que las dos veces pulse la roja tiene que ocurrir que la primera vez pulse la roja
y la segunda también pulse la roja, es decir que se verifique el suceso (R1∩R2).
Ahora bien , como ambos sucesos son independientes, la probabilidad de laintersección es igual al producto de las probabilidades de ambos sucesos. Laprobabilidad de estos sucesos se determina mediante la regla de
Laplace de casosfavorables (uno), partido por casos posibles (tres)
P(R1∩R2) = P(R1) · P(R2) = 1/3 · 1/3 = 1/9
b)En este apartado, claramente, nos piden la probabilidad de la unión de los sucesos
pulsar azul la primera vez y pulsar azul la segunda. Ahora bien, estos dos sucesos no
son incompatibles, luego la probabilidad de la unión será igual a la suma de las
probabilidades menos la probabilidad de la intersección. La probabilidad de la
intersección, al igual que en el apartado anterior, se calcula basándonos en el hecho
de que son independientes.
P(A1∪A2) = P(A1) + P(A2) – P(A1∩A2) = 1/3 + 1/3 – 1/9 = 5/9
Calcule y escriba en una tabla la distribución de la variable aleatoria suma de los números
que aparecen al lanzar dos dados.
Solución.
A continuación presentamos todos los sucesos que pueden ocurrir al lanzar dos dados
y el valor que para cada uno de estos sucesos tiene la variable suma:
(1,1) 2 (2,1) 3 (3,1) 4 (4,1) 5 (5,1) 6 (6,1) 7 (1,2) 3 (2,2) 4 (3,2) 5 (4,2) 6
(5,2) 7 (6,2) 8 (1,3) 4 (2,3) 5 (3,3) 6 (4,3) 7 (5,3) 8 (6,3) 9 (1,4) 5 (2,4) 6
(3,4) 7 (4,4) 8 (5,4) 9 (6,4) 10 (1,5) 6 (2,5) 7 (3,5) 8 (4,5) 9 (5,5) 10 (6,5) 11
(1,6)) 7 (2,6) 8 (3,6) 9 (4,6) 10 (5,6) 11 (6,6) 12
Como todos estos sucesos tienen la misma probabilidad 1/36, la distribución de la
suma será:
X 2 3 4 5 6 7 8 9 10 11 12
P 1/36 2/36 3/36 4/36 5/36 6/36 5/36 4/36 3/36 2/36 1/36
2.2- Un jugador afirma que al lanzar dos dados es igual de probable obtener un seis que un
siete, ya que hay el mismo número de resultados a favor de un resultado que de otro. Cinco y
uno, cuatro y dos, tres y tres, para el seis y seis y uno, cinco y dos, cuatro y tres, para el siete.
¿Es cierta esta afirmación? Razone la respuesta.
Solución.
No, en realidad los sucesos que dan origen a que la suma valga 6 son: (1,5) (2,4)
(3,3) (4,2) (5,1) por tanto la probabilidad será 5/36, mientras que los sucesos que hacen que
la suma sea 7 son (1,6) (2,5) (3,4) (4,3) (5,2) (6,1) y en consecuencia esta probabilidad
será 6/36.
2.3- Para estudiar si las ratas tienen visión cromática, en una caja que cuenta con tres
palancas se marca en rojo aquella que al pulsarla proporciona alimento. En cada prueba la
posición de este pulsador se cambia aleatoriamente. Se somete una rata a cuatro pruebas.
¿Cual sería la distribución de la variable aleatoria número de pulsaciones que consiguen
alimento, si la rata no distinguiera el rojo y pulsase al azar?
Solución.
La variable aleatoria número de pulsaciones puede tomar los valores 0, 1, 2, 3 y 4. El
suceso que da origen a que la variable valga 0 sería
(R,R,R,R)cuya probabilidad sería 2/3 · 2/3 · 2/3 · 2/3 = 16/81
El suceso que da origen a que la variable valga 1 sería:
(R,R,R,R)U (R,R,R,R)U (R,R,R,R)U(R,R,R,R) y su probabilidad sería 4 · 1/3 · 2/3 · 2/3 · 2/3 = 32/81
El suceso que es la imagen inversa de 2 es:
(R,R,R,R)U (R,R,R,R)U(R,R,R,R)U(R,R,R,R)U(R,R,R,R)U(R,R,R,R)
y su probabilidad 6 · 1/3 · 1/3 · 2/3 · 2/3 = 24/81
La imagen inversa de 3 es:
(R,R,R,R)U(R,R,R,R)U(R,R,R,R)U(R,R,R,R) y su probabilidad 4 · 1/3 · 1/3 · 1/3 · 2/3 = 8/81
La imagen inversa de 4 es el suceso:
(R,R,R,R)y su probabilidad es 1/3 · 1/3 · 1/3 · 1/3 = 1/81
Resumiendo la distribución del número de aciertos es:
X 0 1 2 3 4
P 16/81 32/81 24/81 8/81 1/81
2.4- Un jugador de Rol, en una partida de Dungeons and Dragons, para salvarse de un
conjuro de Raistlin, necesita sacar un 18 en el lanzamiento de los dados. El Dungeon Master
le ofrece lanzar tres dados de seis caras o uno de diez junto con uno de ocho. ¿En cual de
estas dos alternativas es más probable obtener un 18 y salvarse del conjuro? Explique su
respuesta ¿Sería la respuesta la misma si hubiese que sacar 17 o más para evitar el conjuro?
Solución.
Para sacar 18 con tres dados de seis caras tiene que ocurrir el suceso (6, 6, 6) que
tiene una probabilidad 1/6 · 1/6 · 1/6 = 1/216.
Para obtener 18 con un dado de diez caras y otro de ocho tiene que ocurrir el suceso (10, 8) cuya probabilidad es 1/10 · 1/8 = 1/80. Obviamente esta probabilidad es mayor que la anterior.
Para obtener 17 o más con los tres dados tiene que ocurrir el suceso:
5, 6, 6)∪(6, 5, 6)∪(6, 6, 5)∪(6, 6, 6) cuya probabilidad es 4/216.
Para conseguir el mismo resultado con los dos dados tiene que ocurrir:
(10, 7)∪(9, 8)∪(10, 8) que tiene una probabilidad de 3/80 que también sería mayor que
con los tres dados.
2.5- Tenemos una urna con dos bolas blancas, tres verdes y cinco rojas. Extraemos al azar
dos bolas simultáneamente. Recibimos 200 pesetas si las dos bolas son blancas, 100 si las
dos son verdes y 10 si una es roja y la otra verde, en los demás casos no recibimos nada.
¿Cual es el valor esperado de los premios?
Solución.
P(B1∩B2) = P(B1) · P(B2 / B1) = 2/10 · 1/9 = 2/90 = 1/45
P(V1∩V2) = P(V1) · P(V2 / V1) = 3/10 · 2/9 = 6/90 = 1/15
P((R1∩V2)∪(V1∩R2)) = P(R1∩V2) + P(V1∩R2) = 5/10 · 3/9 + 3/10 · 5/9 =15/90 + 15/90 = 1/3
Por consiguiente el premio esperado sería:
E[premio] = 200 · 1/45 + 100 · 1/15 + 10 · 1/3 + 0 · 26/45 = 14,4
2.6- En el punto de partida de un laberinto hay tres orificios iguales A, B y C. Si la rata elige
A vuelve al punto de partida después de recorrer dos metros. Si elige B recorre cinco metros
y vuelve al mismo punto. Si elige C sale al exterior recorriendo un metro. ¿Por término medio
que distancia recorre una rata antes de salir, si siempre elige un orificio distinto de los
seleccionados en veces anteriores?
Solución.
Los itinerarios que pueden darse con las distancias recorridas en cada caso, son (A,
B, C) 8, (B, A, C) 8, (A, C) 3, (B, C) 6, (C) 1, y sus probabilidades serían:
P(A, B, C) = P(A) · P(B/A) · P(C/A∩B) = 1/3 · 1/2 · 1 = 1/6
P(B, A, C) = P(B) · P(A/B) · P(C/B∩A) = 1/3 · 1/2 · 1 = 1/6
P(A, C) = P(A) · P(C/A) = 1/3 · 1/2 = 1/6
P(B, C) = P(B) · P(C/B) = 1/3 · 1/2 = 1/6
P(C) = 1/3
En consecuencia la distancia media recorrida será:
E[D] = 8 · 1/3 + 6 · 1/6 + 3 · 1/6 + 1 · 1/3 = 4,5
Tema 6. Descripción de la distribución de frecuencias
Problemas resueltos del Tema 6
1.- Los datos siguientes corresponden a los tiempos de reacción de una muestra de 33
sujetos, medidos en centésimas de segundo:
55, 51, 60, 56, 64, 56, 63, 63, 61, 57, 62, 50, 49, 70, 72, 54, 48, 53, 58, 66, 68, 45, 74,
65, 58, 61, 62, 59, 64, 57, 63, 52, 67.
Calcule la media, mediana, el primer y el tercer cuartil, directamente a partir de los
datos.
Solución:
a)
Para calcular la media simplemente sumamos todos los valores, lo cual da como
resultado 1963, y dividimos entre el número de observaciones que es 33, con lo cual
obtenemos:
48
,
59
33
1963
=
=
x
b)
Para calcular la mediana, el primer paso es escribir los valores en orden creciente:
45, 48, 49, 50, 51, 52, 53, 54,
55
, 56, 56, 57, 57, 58, 58, 59,
60
, 61, 61, 62, 62, 63, 63,
63,
64
, 64, 65, 66, 67, 68, 70, 72, 74
Como el número de observaciones es impar el valor central, es decir el decimosexto, es
la mediana, por consiguiente la Mediana de esta distribución es 60.
El cálculo del primer cuartil es análogo, es la observación que deja una cuarta parte de
las observaciones por debajo y tres cuartas partes por encima, luego en este caso es la
novena observación y por consiguiente el valor del primer cuartil es 55.
Análogamente el tercer cuartil es el valor que ocupa en la anterior ordenación la
posición vigesimoquinta y es 64.
http://www.vitutor.com/pro/3/b_f.html
http://www.ub.edu/stat/GrupsInnovacio/Statmedia/demo/Temas/Capitulo3/B0C3m1t6.htm
http://es.wikipedia.org/wiki/Media_aritm%C3%A9tica






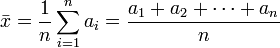
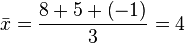
![\sqrt[n]{x_1 x_2 \dots x_n} \le \frac{x_1+ \dots + x_n}{n}](http://upload.wikimedia.org/math/8/e/6/8e601c29ce3964e378346560bff6a281.png)


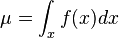




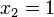






![\sigma = \sqrt{\frac{1}{5} \left [ (4 - 6,33)^2 + (1 - 6,33)^2 + (11 - 6,33)^2 + (13 - 6,33)^2 +(2 - 6,33)^2 + (7 - 6,33)^2 \right ] }](http://upload.wikimedia.org/math/0/1/e/01e64c2ef1d79016de1720f766c87a59.png)
![\sigma = \sqrt{\frac{1}{5} \left [ (-2,33)^2 + (-5,33)^2 + 4,67^2 + 6,67^2 + (-4,33)^2 + 0,67^2 \right ] }](http://upload.wikimedia.org/math/0/3/a/03a16df6f28dc3cadbdae3393fe43bfb.png)



espero que sea de mucha ayuda este trabajo y sea apreciable para los lectores.
ResponderEliminar